IFS Data Deconvolution

Abstract: We perform a PSF deconvolution on the SDSS-IV MaNGA integral field unit (IFU) data to mitigate beam-smearing and atmospheric seeing effect. We use wavelength-dependent PSF size information to perform the deconvolution. We test the PSF deconvolution method to the mock IFU data and show that the deconvolved IFS data by this method can reasonably well recover correct kinematic parameters. Deconvolution performance is depending on radial coverage and S/N distribution of an IFS data. The method can be applied to other type of IFU data as well.

[Update Aug. 11th, 2020] Manuscript submitted to ApJS, and currently available at arXiv ( https://arxiv.org/abs/2008.04313)

Example Python3 code can be found at https://github.com/astrohchung/deconv

Light from the sky to a ground-based telescope always pass through the atmosphere, and turbulence of the atmosphere blurs light from a point source to the shape of a point spread function (PSF), which called as atmospheric seeing effect. This effect correlates spatial information of extended objects and limits a detailed spatially resolved study of the objects. There are ways to overcome this seeing effect using 1) space telescope, or 2) adaptive optics but, the resources are limited. Thus, most of ground-based telescopes are still being suffered by the seeing effect.

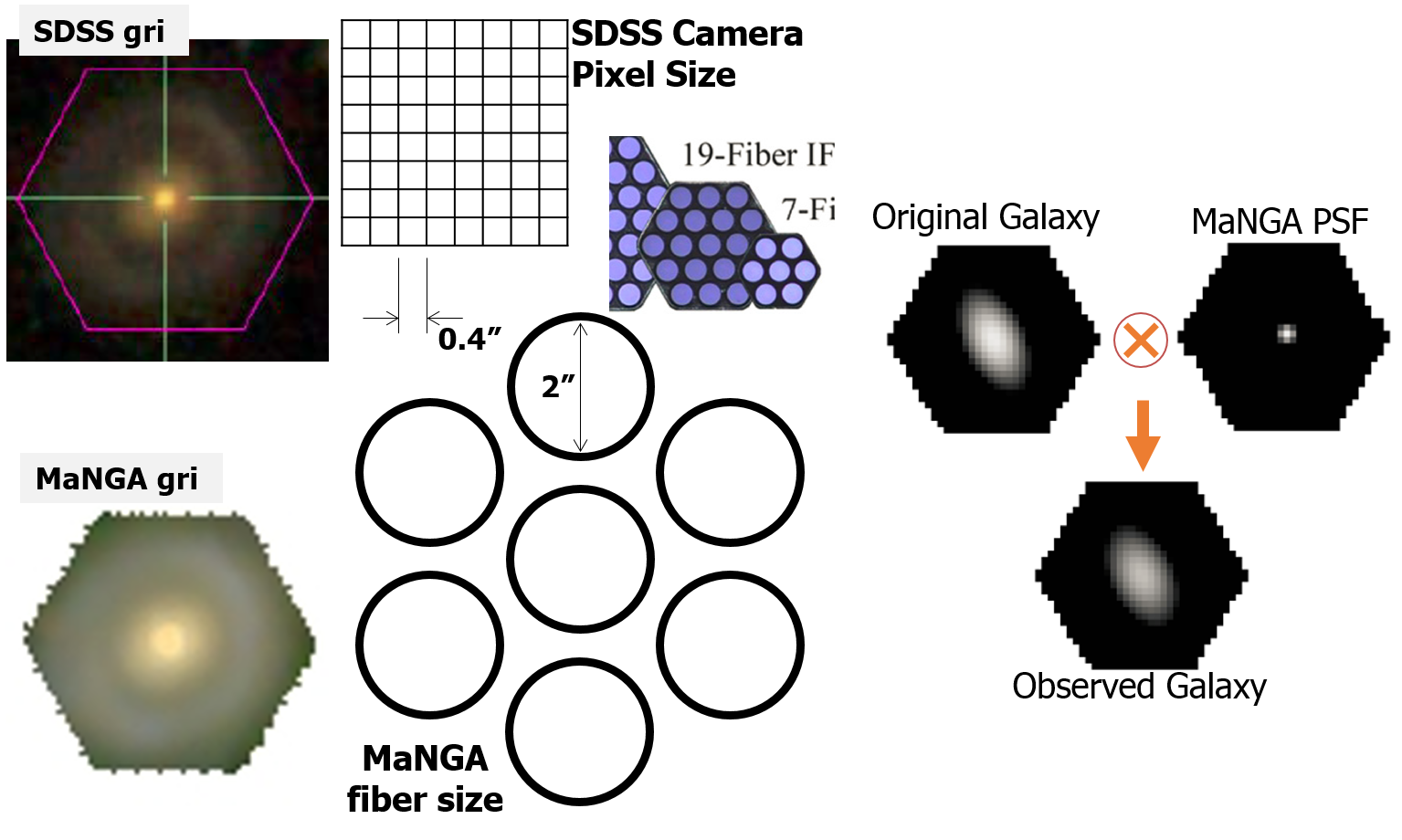
In the field of fiber-based integral field spectroscopy, the situation becomes worse due to the large sampling size of the fibers. In case of SDSS-IV MaNGA IFU survey data (Bundy et al. 2015), the fiber sampling size causes undersampling of the astronomical targets and produces effective PSF full width at half maximum (FWHM) with about 2.5". This is larger than typical atmospheric seeing size (1.5") (ref) at the Apache point observatory. Although MaNGA made a set of three dithered exposure to relieve the undersampling issue, the effect of seeing and beam-smearing remain in the reduced data. For example, in case of SDSS-IV MaNGA data, the direct comparison of gri image from SDSS imaging camera and reconstructed gri image from MaNGA IFU shows the difference in image quality due to sampling size. Here we call combined effect of seeing and beam-smearing as a PSF effect.

There were many attempts to minimize impacts of the PSF effect on their scientific results. An approach is convolving a PSF on a model before comparing with observed data. Another approach is estimating an impact of seeing on the derived parameter by forward modeling. By using forward modeling, it is possible to find a relation between PSF size with a paticular measured parameter. (See Graham et al. 2018 for spin parameter measurement) However, the first approach requires PSF convolution on each model and the second approach requires forward modeling on each parameter, both demand a considerable computational power and time.

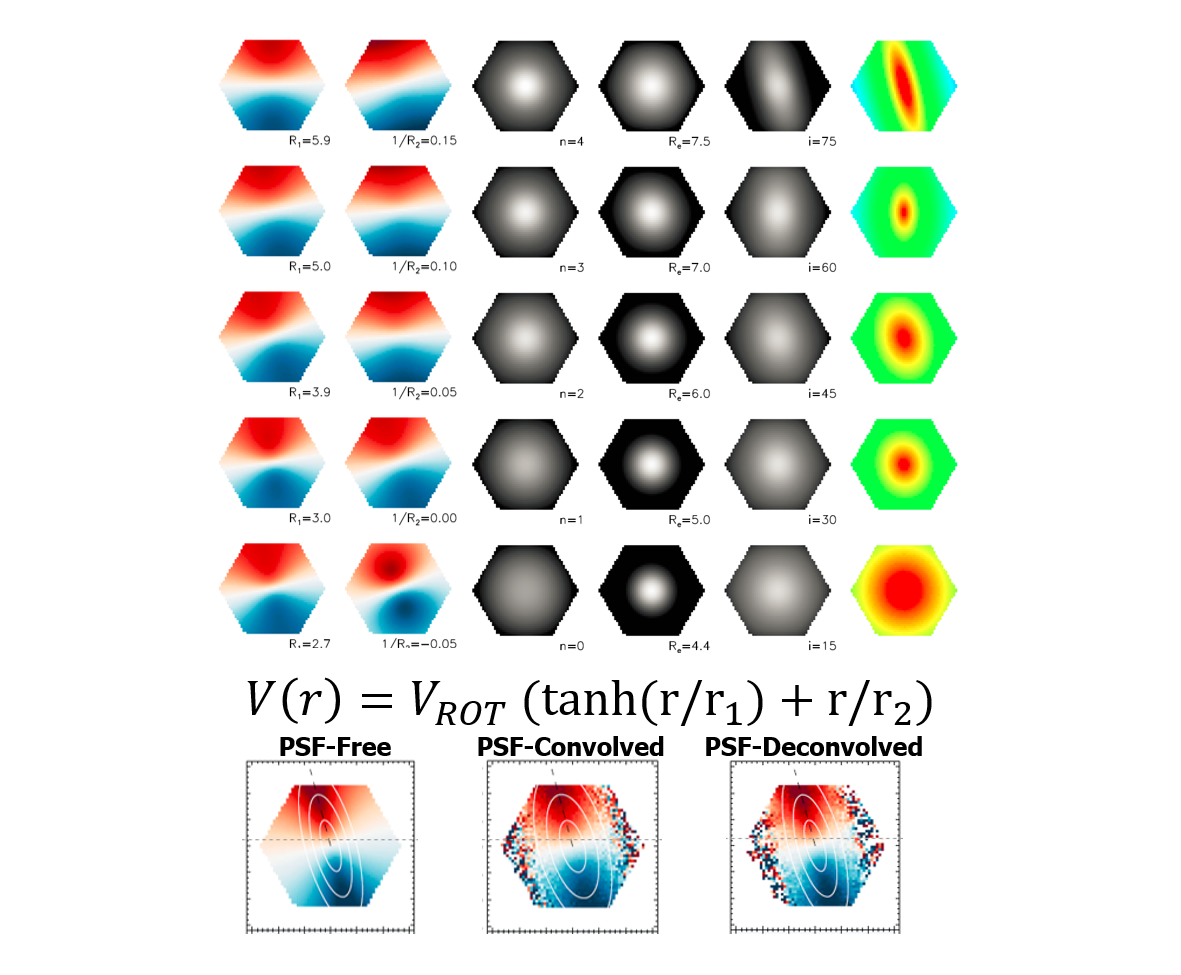
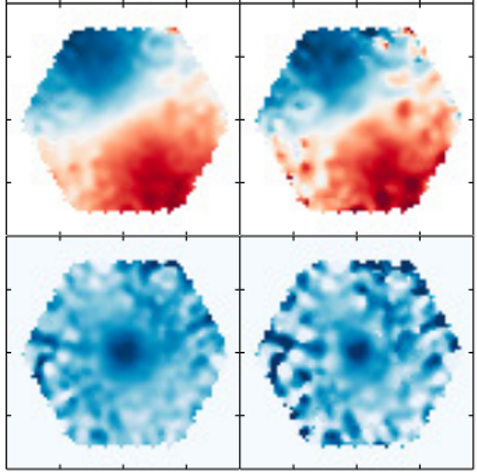
We propose a new method to mitigate the PSF effect on IFU data using PSF deconvolution. This method deconvolves the IFU data at each wavelength bin using gaussian shape PSF. It applies Richardson–Lucy algorithm (Richardson 1972) and deconvolves the IFU data at each wavelength bin using a gaussian shape PSF. In case of MaNGA IFU data, FWHM of PSF at four bands (griz) are used to define the gaussian shape PSF. FWHM values are provided along with an each IFU data from observation of stars with 12 mini-IFUs (7 fibers). By applying this method, we have found that PSF-deconvolved data shows noticable difference compared with PSF-convolved data.

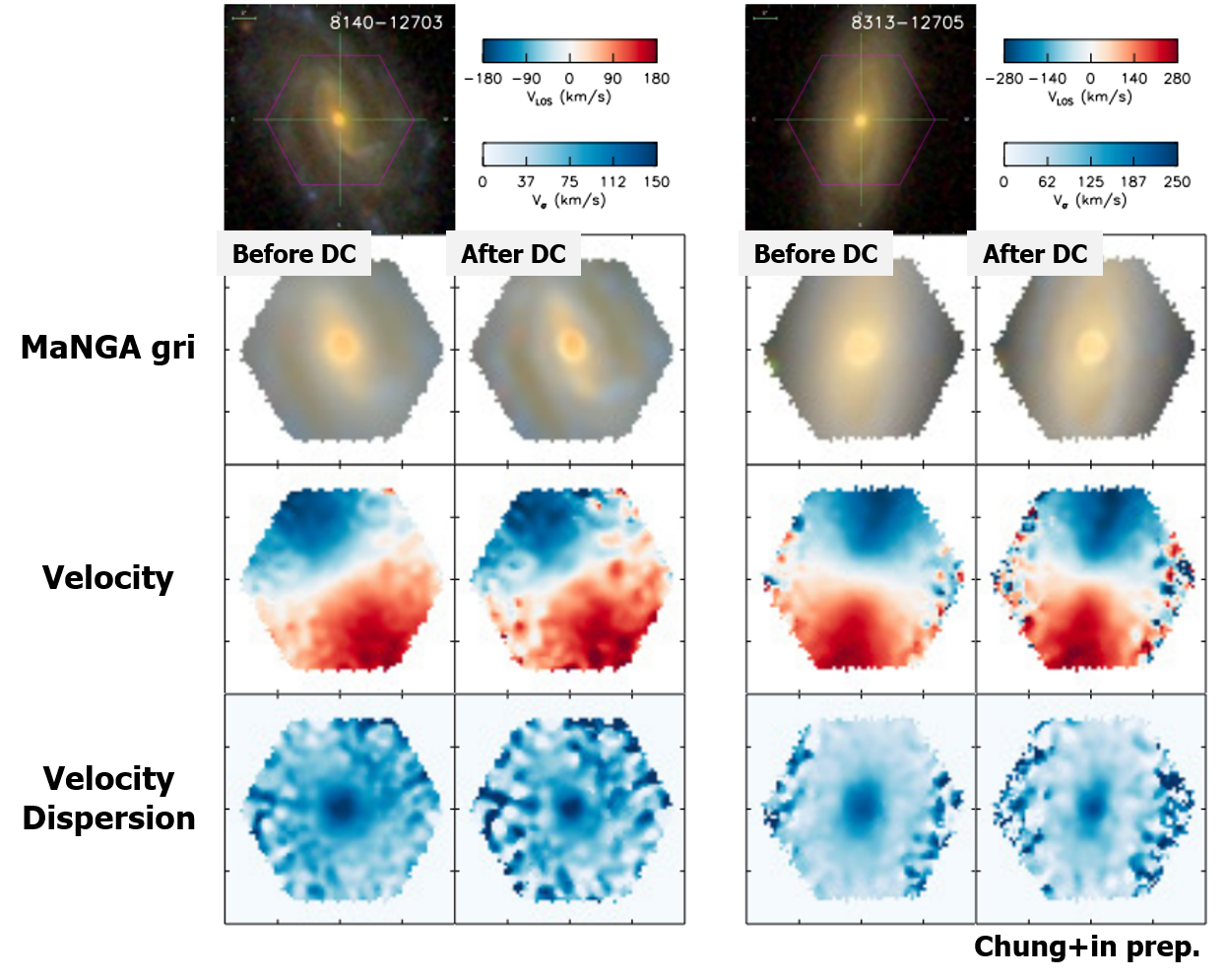
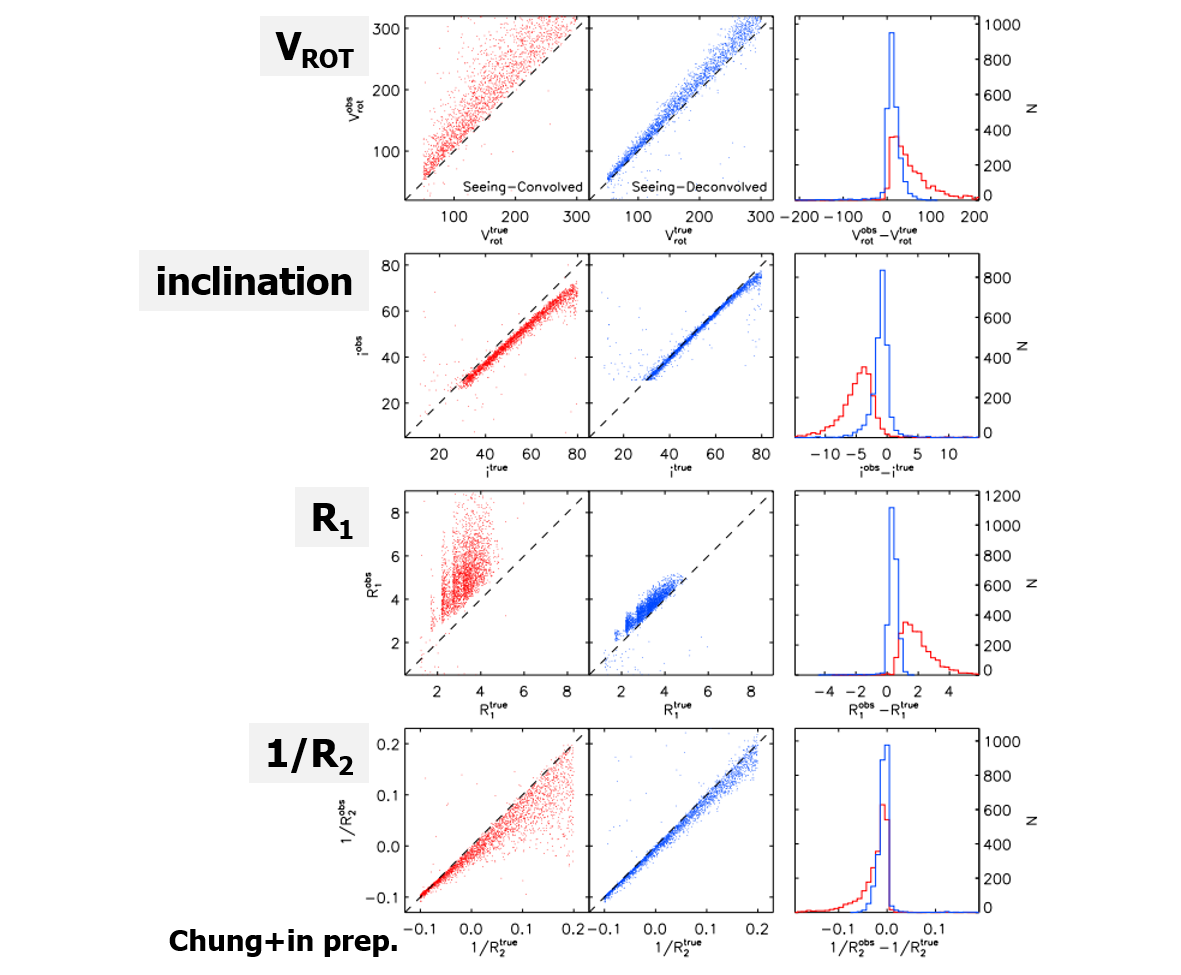
We performed comprehensive tests to quantitatively check the effect of our method. We construct a PSF-free mock of MaNGA IFU data using a set of geometrical parameter, light distribution, signal to noise ratio distribution, stellar kinematic model, and synthetic stellar population. From a set of PSF-free mock, we produce PSF-convolved mock data by convolving wavelength dependent gaussian PSF and adding Poisson noise. We apply our deconvolution method to the PSF-convolved mock data and generate PSF-deconvolved mock IFU data. We measure kinematic model parameters from three different kinds of mock IFU data (PSF-free, PSF-convolved, and PSF-deconvolved), and compare them with each other. The result shows that the kinematics parameters measured from PSF-deconvolved mock IFU data is well-matched with those from PSF-free mock IFU data, while those from PSF-convolved mock data are not. We conclude that the PSF deconvolution method is an efficient way to convert PSF-convolved data close to PSF-Free one. Outcome of this method can be used directly for comparison with a model or measurement of a certain parameter, without an additional process.

In order to demonstrate the validity of the deconvolution method quantitatively and estimate the limitation of this method, we are performing additional tests with the mock MaNGA IFU data. We are expected to apply this method for general data analysis of integral field spectroscopy. The deconvolution code in Python3 will be publicly available soon through Github with a tutorial.